Droplet size and surface area
Droplet size is often critical. Many processes such as gas scrubbing depend on exposing the maximum possible amount of liquid surface to a gas stream. Other applications require that the droplets be as large as possible, such as when the spray must project into a fast moving gas stream.
Exposing the maximum surface area requires breaking the liquid into droplets as small as possible. For any given volume of fluid being sprayed the surface area exposed is inversely proportional to the droplet size. So if one halves the droplet radius one doubles the surface area of the fluid; if one quarters it one quadruples the surface area.
To see why imagine a cube of water 1 metre cubed.
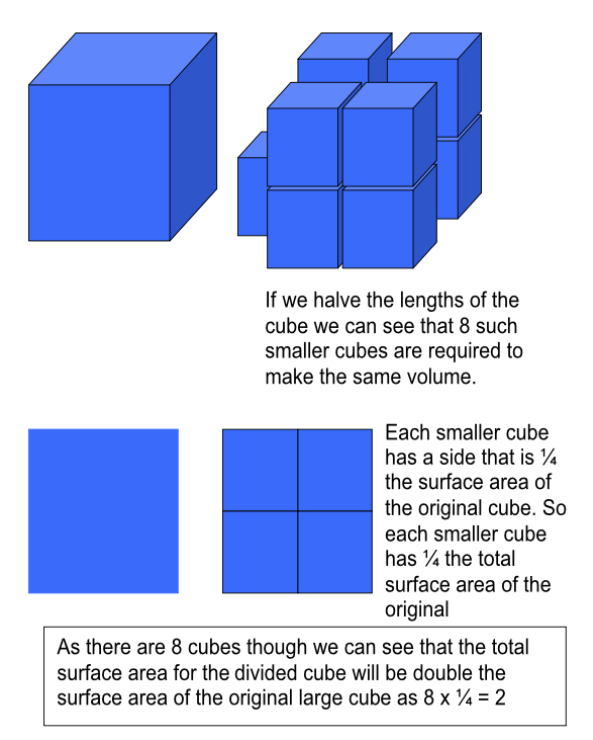
The principle above works for any uniform geometric shape. So as long as a shape is broken up into similar but smaller shapes the principle will hold. The droplets that make up a fluid are all more or less the same shape (roughly spheres) and any variations in shape will average out over a large number of droplets meaning that the principle above holds well for sprays in real life. Halve the droplet size and double the surface area, third the droplet size and triple the surface area, quarter droplet size and quadruple etc etc.
So the rule is:
Halve the droplet radius = double the surface area
Or more generally:
Reducing the droplet radius by a factor of N will multiply the surface area by a factor of N