Efficient Tank Cleaning

Note: The Pdf version of this article can be downloaded by clicking icon to the right
The
cleaning of tanks and vessels is often an overlooked source of inefficiency in the manufacturing process. Contamination through poor cleaning can result in the loss of an entire batch of product or, worse, a product recall. The cost of failure can
be very high and so many quality control managers will be highly reluctant to consider more efficient methods of cleaning.
This article explores ways of reducing water consumption, chemical usage, energy consumption and the time taken in tank cleaning applications without compromising overall cleaning effectiveness.
What makes a clean effective?
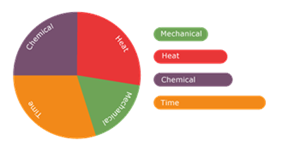
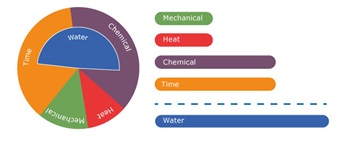
Any cleaning application has four components that contribute towards its effectiveness.
1- Time. The longer the cleaning if performed the greater the cleaning.
2- Chemicals. This is the dissolving effect of chemical cleaning fluids including water.
3- Mechanical action. This is physical action of the cleaning spray to dislodge residue.
4- Heat. Generally the hotter the cleaning fluid the better the cleaning action.
Increasing any of these 4 components will improve overall cleaning but there will be a cost associated with each. The cost of each of these elements will differ depending on application and there may well be other constraints in place. For example,
in food processing applications there will be limits on the types of chemical that can be applied.
Understanding the differential cost of each element is the key to efficient cleaning. Optimising the mix of elements is the process of increasing one element of the mix that has a lower cost (e.g. mechanical action) so that another element that has a
higher cost (e.g. heat) can be reduced. The net cleaning power will remain the same but the cost associated with the cleaning process will be reduced.
The relative contribution of each of the 4 elements of the cleaning mix can be represented on a Sinner Circle diagram as shown below.
Absolute efficiency gains
Whilst overall efficiency can be gained by reconfiguring the contributions from each element it is clearly beneficial to strive for efficiencies in each element. If, for example, a cheaper method of heating can be found then this element in its own right
becomes more efficient, and thus the whole process is more cost effective. This would be an absolute efficiency gain as the same cleaning power is delivered using less overall resource.
An absolute gain in one element, however, might be
better utilised by reducing the contribution from another more costly element. For example, if a more efficient heating method were found then either heat could be maintained at the current level for a lower cost OR heat could be increased for the
same cost. If heat is increased then perhaps time could be reduced whilst keeping overall cleaning power at the same level. If the opportunity cost saved by reducing cleaning cycle time is greater than
the savings made by improved heating efficiencies
then this configuration is optimum. In other words, a gain in efficiency in one element is not always best deployed in that element.
Water efficiency
“Water” is not one of the 4 elements of the mix but water usage clearly is an important factor. The amount of water used in any cleaning mix depends mostly on the role of the chemical element and the time element. Water is known as the universal
solvent as it dissolves more substances than any other liquid. As such it often makes up all or the majority of the chemical component of the cleaning mix.
It should also be obvious how a reduction in the time component of the cleaning mix will reduce water consumption. The shorter the cleaning cycle is the less water will be used.
Reducing water usage is a key driver for many businesses because it is an easy way to measure efficiency. Estimating the true cost benefit of improved time or reductions in chemical action or heat can be hard. The benefits are sometimes hard to measure
and quantify. Water usage, however, is easy to measure. As we know that water consumption does equate to the “time” and “chemical” element we can use it as a proximate measure of tank cleaning efficiency in many cases.
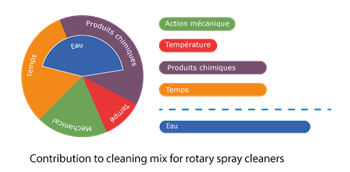
As water usage is such a useful measure of efficiency it is worth modifying the Sinner Circle diagrams to include a measure of water consumption for each tank cleaning situation. Examples of these modified Sinner diagrams are shown below.
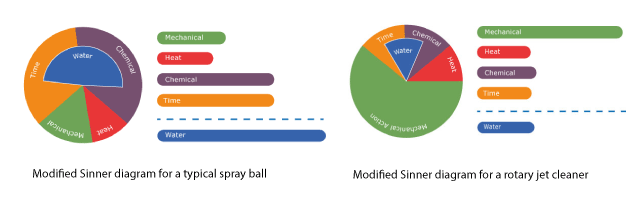
Water is money
The true cost of water is often under appreciated.
• Raw utility bill cost per m3 of water
• Cost of filtering and sanitising if recycling wash off
• Cost of caustics or other cleaning fluids
On top of this if we reduce the water needed to clean we can
• Lower pump running costs (electricity)
• Lower maintenance costs
• Longer lifetime for the pump
• Potentially use a smaller pump (reduced capex)
As the cost of energy and water are both increasing, and likely to continue to increase, reductions in water usage have significant financial benefits to any organisation. Furthermore, the green/environmental benefits are seen as a moral imperative by many organisations. Future green legislation is only likely to increase the need for more efficient water usage.
Time efficiency
Time is money. It may be a cliché but it’s still true. The time spent cleaning between production runs, whilst necessary, still represents downtime. This is time that the vessel can not be used for production. The opportunity cost associated with this downtime will vary greatly depending on the application, but in almost all cases a reduction on cleaning cycle time will have a direct financial benefit. Reducing cleaning time could allow for another batch to be produced per week or per month so the cost of having a longer cleaning cycle is equivalent to the value of the “lost” product.
Chemical efficiency
As discussed above the biggest savings in the chemical element come from reducing water consumption. But, in addition to water reduction, lowering the use of caustics and other cleaning chemicals can be a key driver for many businesses. Cleaning chemicals are expensive to buy and also can incur considerable disposal costs as well. Typically a reduction in the chemical element of the cleaning mix will be compensated for by improved mechanical action and/or heat.
Heat efficiency
Heat improves the chemical action element of the cleaning mix. Heated water and caustics will act more quickly to dissolve and break up residues. As such the amount of each can be reduced and still contribute the same amount of cleaning power. Of course, such savings are not absolute gains because they need to be offset against the energy cost of heating the fluids.
Mechanical Action - The quick win
Often the simplest absolute efficiency gains can be found by improving the mechanical action element of the mix. These gains can then be deployed to reduce other elements of the mix as appropriate.
The importance of nozzle selection
For any impact cleaning process water serves two purposes. Firstly it acts to dissolve residue - this is part of the chemical element of cleaning mentioned above. More importantly, however, water is the mechanism by which the mechanical action element is delivered. The efficiency of a water spray for delivering mechanical energy for cleaning will be greatly affected by the nature of the spray and thus the nozzle used.
Improving the efficiency of mechanical action
Mechanical action is essentially the process of transferring energy from a pump to the surface to be cleaned via water. As with all energy transfer systems efficiency is always less than 100%. Much energy is wasted but by reducing this waste through improved nozzle selection we can significantly improve the efficiency of the tank washing system. If this is achieved then we can reduce the amount of energy/water used and achieve the same or greater level of mechanical action.
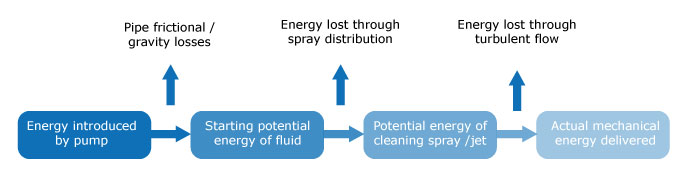
The Effects of Fluid breakup
The process of breaking apart a fluid into droplets or multiple streams to form a spray pattern uses energy. This, once used, is then not available for cleaning the surface in question. In tank cleaning applications fluid will be delivered in 3 basic spray patterns.
Solid stream – this is a simple jet of water and will impact the tank surface as a small dot. Solid stream nozzles do not atomise the fluid and it remains as a constant stream of liquid. As such they preserve the majority of the energy resulting in maximum impact

Flat fan – The fluid is widened into triangle shaped spray. It will impact the surface as a thin line of spray. Fan nozzles generally produce a sheet of fluid with little atomisation, although some droplets will form. The formation of the sheet and the droplets takes a considerable amount of energy out of the liquid meaning impact is medium.
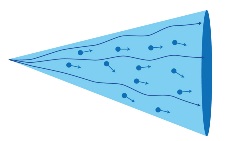
Full Cone – The fluid is again widened into a cone shape and there is a relatively even distribution of fluid within the cone. It will thus hit the tank walls as a filled in circle of spray. A large degree of atomisation occurs with this pattern meaning almost all the energy is used to break the fluid apart. This means the impact on the tank wall is minimal.

Turbulence
Further energy will be lost in sprays due to turbulent flow. In solid stream and, to a lesser degree, flat fan nozzles the fluid will be flowing in an unatomised state. This does not, however, mean that all the liquid is moving in a uniform direction at all times. Ideally we would want every water molecule to move in the direction of the stream. This idealised motion would result in the most efficient energy transfer. This perfect laminar flow is best for energy transfer. The more turbulent the flow becomes the more energy is wasted and the more the stream starts to break up.
As a result of turbulence not all solid stream flows are equal when it comes to energy transfer. The quality of the stream will depend very much on the quality of the nozzle forming it. With spray balls the multiple streams formed are technically solid streams but the nozzle that forms them is simply a hole in a metal sphere and so are low quality. The resultant streams are unstable and lack coherence and, as such, they tend towards turbulent flow very quickly. In contrast the jets formed by rotary tank cleaners will be formed by long nozzles with flow stabilisers built in This means that these streams will remain laminar for longer.
Not all solid streams are equal
The diagrams below illustrate how turbulence and stream breakup can vary between different solid stream jets.
Idealised laminar flow. This will give the maximum energy transfer.

Good laminar flow. Typical flow from high-quality nozzles. The jet will maintain integrity at a good distance from the nozzle. Energy transfer is good.

Poor laminar flow. Typical flow from spray balls and low-quality nozzles. The jet will quickly break up and energy transfer is poor.

Notes on pressure
It would seem logical that increasing pressure will improve the mechanical action of any tank washer. This, however, is only partly true. For cone pattern and the flat fan patterns formed by spinning spray balls if the pressure goes much above 1.5-2 bar little gains in impact will be delivered. This is because the flows are so unstable
that most of the extra energy will be used to atomise or break up the fluid. The extra energy put into the system is effectively wasted.
Similarly, the nozzles that form the streams on spray balls will produce very unstable jets. As pressure goes beyond a couple of bar the instability of the jets means that they will tend to atomise and break up. So, again, energy just tends to be wasted in running spray balls at higher pressures.
With rotary jet nozzles the story is somewhat different. As they use flow stabilising nozzles most will hold coherent jets at 10 bar or more. Above this, though, there will be diminishing returns as even these quality streams will begin to break apart at higher velocities. Increasing pressure will also decrease the cycle time as the jetting arms will rotate faster. At higher pressures, the jets may be rotating so fast that this perpendicular motion causes the stream to loose coherence. Normally the optimum pressure for rotary jet nozzles is about 8-10 bar.
Mechanical action - conclusions
The most efficient spray system would be solid stream jet followed by a flat fan spray pattern and finally a full cone pattern. Spray balls, despite forming multiple mini solid streams are best considered as full cone patterns in terms of energy transfer efficiency.
The efficiency differences are considerable. Changing from spray balls to solid stream nozzles will result in a dramatic increase in mechanical action for the same flow
rates of water. This is an absolute gain in efficiency that can greatly affect the overall efficiency of the tank clean.
Designs of tank washing nozzle
These nozzles are spheres with multiple holes producing an omnidirectional spray. The jets from each individual hole do approximate to a solid stream but the spray pattern is best approximated to a full cone spray rather than solid stream. This is for the following reasons:
1- The holes in the spray balls are only very crude nozzles meaning that laminar flow in the resulting jets is limited. This is because only the thickness of the spray ball wall is present to form a coherent water jet. The streams that result break up easily and, generally, do not travel very far before breaking up.

2- The energy and water is divided. The water is split into scores of individual jets and so the energy of each is reduced. This means that each jet lacks momentum and reach.
What this means is that spray balls result in almost no meaningful impact on the walls of the tank. The vast majority of their cleaning power comes from the solvent properties of water cascading down the walls the tanks. This often needs to be boosted by the addition of cleaning chemicals or needs to be enhanced by long cleaning cycle times. In terms of water efficiency this type of cleaning is normally highly inefficient unless only very light and water soluble residues are being cleaned
These nozzles produce a “cone” of spray up to 270o wide. This makes them suitable for cleaning tanks by inserting them towards the top of the vessel. The spray is cone and thus inefficient at energy transfer.
Various nozzle manifold tank cleaners exist on the market. Several full cone nozzles will be positioned on a single head giving an omnidirectional spray. Because multiple nozzles are being used to produce more direct sprays the impact per volume of water is increased. However, the individual sprays are still full cones consisting of droplets and thus inherently inefficient. Such systems are suitable for small-medium sized tanks that require light to moderate cleaning.
These nozzles will have several flat fan sprays that rotate under the pressure of the fluid. The rotating fans will sweep the whole of the tank. As with static nozzles complete coverage happens only after a few moments but the nozzle spray will need to be working for while before any significant residue is removed. As
a flat fan pattern is being used there is a moderately efficient energy transfer
resulting in a medium impact cleaning spray.
 These nozzles are often the most efficient choice for small to medium sized tanks that have moderately stubborn residues to remove.
These nozzles are often the most efficient choice for small to medium sized tanks that have moderately stubborn residues to remove.
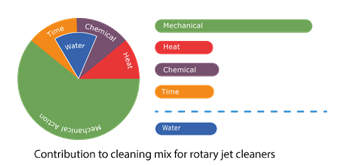 These machines have 2,4 or 8 solid stream jets which rotate sweeping the inside of the tank. A gearing mechanism changes the angle of the rotation so over time complete cleaning of the tank is achieved.
These machines have 2,4 or 8 solid stream jets which rotate sweeping the inside of the tank. A gearing mechanism changes the angle of the rotation so over time complete cleaning of the tank is achieved.
These nozzles are by far the most energy efficient tank washers due to the solid stream jets being deployed. They are generally more expensive than other types of tank washer but for medium to large tanks or tanks with stubborn residues the additional capital expenditure is often paid for rapidly through efficiency gains.
Cycle times
Unlike the other types of tank cleaner mentioned above rotary jet cleaners need to run through a minimum set cycle time. This is because the jets need to be brought to bear on each part of the tank. Failure to run a complete cycle will mean that parts of the tank are simply not cleaned.
Most rotary jet cleaners are geared to run fairly slowly.  This is so that the jets have sufficient dwell time on each part of the tank to ensure maximum cleaning power. Also if the jets rotate too rapidly they tend to break up causing a loss in mechanical action. What this means is that for many tank cleaning applications rotary jet cleaners rotate too slowly. The mechanical action component is too high, each part is over cleaned but because the set cycle must be completed the overall water usage is higher than necessary. In short the tank is over cleaned, which is wasteful.
This is so that the jets have sufficient dwell time on each part of the tank to ensure maximum cleaning power. Also if the jets rotate too rapidly they tend to break up causing a loss in mechanical action. What this means is that for many tank cleaning applications rotary jet cleaners rotate too slowly. The mechanical action component is too high, each part is over cleaned but because the set cycle must be completed the overall water usage is higher than necessary. In short the tank is over cleaned, which is wasteful.
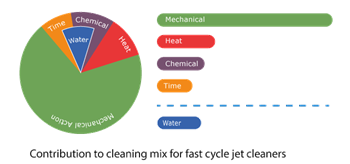 These machines are smaller and lighter rotary jet cleaners that have been geared to run through their cycles much faster than normal. The resultant jets do not have as much dwell time on the surface of the tank and so do lose some of their cleaning power. Also, because they are spinning fast, the jets will tend to break up more rapidly. Nevertheless, these cleaners will still give good mechanical action at distances below 2-3 meters from the nozzle.
These machines are smaller and lighter rotary jet cleaners that have been geared to run through their cycles much faster than normal. The resultant jets do not have as much dwell time on the surface of the tank and so do lose some of their cleaning power. Also, because they are spinning fast, the jets will tend to break up more rapidly. Nevertheless, these cleaners will still give good mechanical action at distances below 2-3 meters from the nozzle.
The fast cycle time means the jet cleaner can deliver a complete tank cleaning in a few minutes. The practical upshot is that for small to mid-sized tanks that have residues that do not require long jet dwell times to dislodge, this class of tank cleaner can offer some water efficiency gains. In effect, this class of tank cleaner is designed to mitigate the limitations imposed by the long cycle times of standard rotary jet cleaners.
Impediments to changing cleaning heads
Different flows and pressures
Most spray balls, spinning spray balls and static nozzles will operate at low pressures between 1 and 3 bar. Flow rates can vary considerably with big spray balls using several hundred litres per minute and small spinner using as low as 20 litres per minute.
Rotary jet cleaners (both standard and fast cycle) tend to operate best between 5 and 10 bar pressure. Flow rates, again, vary considerably and depend greatly on the number of nozzles and pressure. Typically they will operate most efficiently in terms of water used per cleaning cycle at about 8 bar pressure.
Moving from spray balls to rotary jet cleaners will almost certainly improve water efficiency but it may necessitate a change of pump and/or pipe work. The good news is that the new fast cycle jet cleaners will normally be able to run at low pressures (1-2 bar). Their flow rates are often similar to that of existing spray balls so often can just be swapped in without having to change pumps. If this is the case it is still worth considering changing to a higher pressure pump because rotary jet cleaners will do a better job for less water per cycle at higher pressures.
Opening Sizes
Spray balls will typically fit through openings smaller than 75mm. Some larger balls may require 100mm openings to fit through. Spinners are typically even smaller in profile with many models fitting through 50mm openings. Rotary jet cleaners will typically need 125mm plus openings to fit through but the new, smaller fast cycle models can fit through 75mm openings at a squeeze.
If you have openings above 75mm there may be no need to cut the tank to install rotary jet technology. If, however, you have under 75mm clearance then modifications to the tank will need to be made to install the more efficient jet cleaning heads. These might prove costly and so this needs to be taken into account.
ATEX
Spray balls and other static nozzle systems are effectively ATEX exempt. With no moving parts there is no chance of any sparking risk from such tank cleaners. As long as they are conductive and earthed then no charge can build as they are typically stainless steel attached to stainless steel pipes ATEX considerations are minimal.
Rotary jet cleaners and spinning spray balls do need ATEX certification if they are to be deployed in tanks that contain explosive environments. Thankfully there are many ATEX certified models on the market. It is, however, wise to look carefully at the ATEX claims of tank cleaner manufacturers. Getting an ATEX cert is an exhaustive process that covers not just the design of the device but also checks quality control and sourcing procedures to ensure compliance.
Some manufacturers have been known to use ambiguous phrases like “complies with ATEX design” or “ATEX exempt design” rather than simply stating the product is ATEX certified for X zone and Y temperature. If there is any doubt ask for the ATEX certification for the product. Compliance with ATEX is not something to take lightly or to have any ambiguity around. If the ATEX cert has been awarded then the manufacturer should be touting this fact in no uncertain terms because they will have had to go through a rigorous and costly process to get it!
Conclusions
Quick wins can often be found by looking at the mechanical action element of the cleaning mix. The efficiency of the mechanical action delivery mechanism can often be improved by correct cleaning head selection. Typically this will mean upgrading to rotary jet cleaning heads. Many of the historical impediments to installing rotary jet cleaners have been removed by smaller and faster wash cycle models. This means that real absolute efficiency gains in time, water and energy can be achieved with minimal disruption.
These gains can be further multiplied by considering how the 4 elements of the cleaning mix can be reconfigured. It may, for example, be more beneficial to reduce the heating and chemical elements of the mix rather than use all the efficiency gains to reduce water consumption. The optimum configuration of the mix will vary from application to application but regardless improvements in the mechanical action component of the mix are often a quick win with a payback time measured in weeks rather than months.
5 Steps to improve efficiency
Step 1 - Consider the true cost of each of the 4 elements of the cleaning mix.
Step 2 - Consider the current contribution to cleaning from each element.
Step 3 - Look at which elements have absolute efficiency gains to be made.
Step 4 – Look carefully at the potential “quick win” by increasing mechanical action
Step 5 - Assess how the new cleaning mix will be optimised
For more information on tank cleaning heads of all type please visit the tank cleaning section of our website here